Research project studying self-assembly in complex fluids and laboratory class papers.

Linker-mediated phase behavior of DNA-coated colloids
J. Lowensohn, B. Oyarzun, G. Narvaez Paliza, B. M. Mognetti, W. B. Rogers
arXiv,
(2019) https://arxiv.org/abs/1902.08883
The possibility of prescribing local interactions between nano- and
microscopic components that
direct them to assemble in a predictable fashion is a central goal of nanotechnology research.
In this article we advance a new paradigm in which self-assembly of DNA-functionalized colloidal
particles is programmed using linker oligonucleotides dispersed in solution. We find a phase
diagram that is surprisingly rich compared to phase diagrams typical of other DNA-functionalized
colloidal particles that interact by direct hybridization, including a re-entrant melting
transition upon increasing linker concentration, and show that multiple linker species can be
combined together to prescribe many interactions simultaneously. A new theory predicts the
observed phase behavior quantitatively without any fitting parameters. Taken together, these
experiments and model lay the groundwork for future research in programmable self-assembly,
enabling the possibility of programming the hundreds of specific interactions needed to assemble
fully-addressable, mesoscopic structures, while also expanding our fundamental understanding of
the unique phase behavior possible in colloidal suspensions.
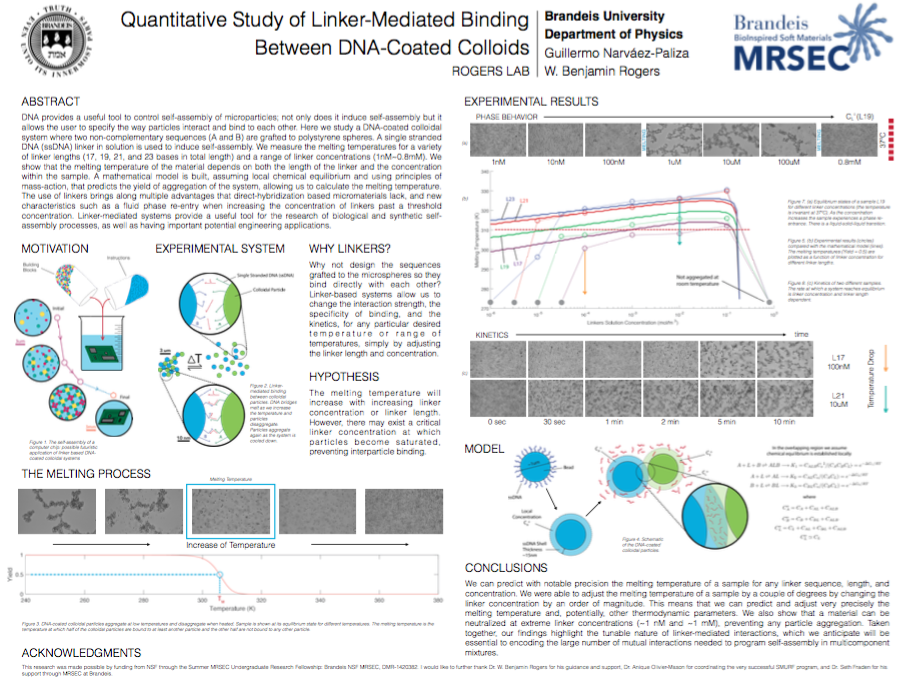
Linker-Mediated Binding Between DNA-Coated Colloids
Poster presentation for Summer Science Research Program at Brandeis University
The use of DNA linkers in combination with colloidal suspensions brings along multiple advantages
that direct-hybridization based micromaterials lack, and new characteristics such as a fluid
phase re-entry when increasing the concentration of linkers past a threshold concentration.
Linker-mediated systems provide a useful tool for the research of biological and synthetic
self-assembly processes, as well as having important potential engineering applications.

Random Walks and Computation
Written for the "Advanced Physics Laboratory" course at Brandeis University.
In the
microscopic world, physical systems are significantly more sensitive to individual
interactions than macroscopic ones. Microparticles tend to follow a diffusive motion rather than
a ballistic motion, making it harder to predict the dynamics of a system. Here we explore the
validity of using computer simulations to substitute real physical systems and predict their
dynamical properties using mathematical and probabilistic tools. We explore flexible polymers in
solution and particles undergoing Brownian motion in a one-dimensional medium and show that the
systems can be safely approximated by numerical methods involving the generation of random
numbers. We show that the anisotropy of flexible polymers’ shapes is mostly due to the random
walk nature of the system and not due to intramolecular interactions or self-avoiding effects.
We show that the Langevine equation can be used to predict the trajectory of a Brownian particle
while ignoring the inertial term, and that a Monte Carlo algorithm can be used to describe more
precisely and at a cheaper cost the properties of an equilibrated system.

Ising Model of Magnetization
Written for the "Advanced Physics Laboratory" course at Brandeis University.
Magnetic
materials can be found everywhere in our daily lives. However, we often think of
magnetic materials to be any material that has some magnetization, i.e. a magnet. What we often
do not consider is that magnetic materials can exist in two different phases, the ferromagnetic
phase and the paramagnetic phase. The ferromagnetic phase is a consequence of the alignment of
magnetic spins that generate a net magnetization, while the paramagnetic phase is a result of
spins being randomly oriented, resulting in a zero magnetization due to the random nature of the
spin configuration. Here we prove through computer simulations that the Ising model can be used
to show the existence of the two magnetic phases. We show that in the one-dimensional Ising
model there is no phase transition, while in the two-dimensional case there exists a transition
around the critical temperature of 2.4 J/k_B.

Chaos
Written for the "Advanced Physics Laboratory" course at Brandeis University.
For many
deterministic systems we can exploit the laws of Physics to make an accurate estimation
of the system state. For example, we can determine the speed of a falling ball at a given moment
if we know the initial conditions and the time at which it was released. However, some systems
that are completely constrained to the laws of Physics, seem to be unpredictable. We call this
systems chaotic. Chaotic systems appear random because the intrinsic uncertainty of the
measurement of the initial conditions grows quickly, specifically as an exponential function. As
time increases, the uncertainty becomes large and predictions innacurate. Here, we explore the
non-linear, damped, driven pendulum, and explore the conditions under which the pendulum
undergoes periodic, semiperiodic, and chaotic motion. We prove resonance and hysteresis in the
driven pendulum and give several characterizations of motion that help us determine if a system
is periodic or chaotic. Finally, we produce a bifurcation plot, which allows us to observe the
phase transition of a system that goes back and forth, from periodic to chaotic.